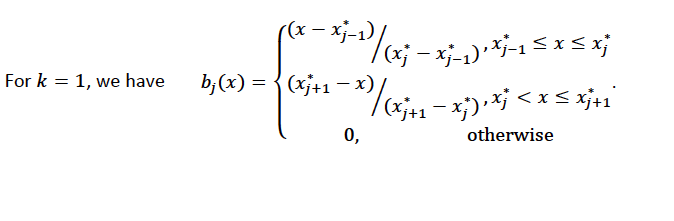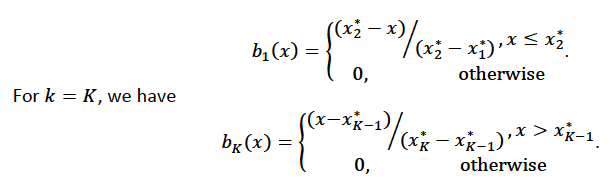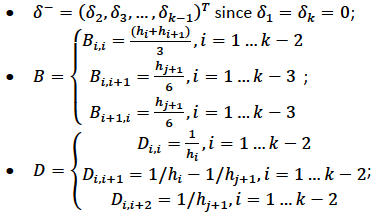Generalized Additive Models (GAM)

Note: GAM models are currently experimental.

Introduction

A generalized additive model (GAM) is a Generalized Linear Model (GLM) in which the linear predictor depends linearly on predictor variables and smooth functions of predictor variables. H2O’s GAM implementation follows closely the implementation as described in “Generalized Additive Models: An Introduction with R, Texts in Statistical Science [1]” by Simon N. Wood. Another good resource for GAM can be found in “Generalized Additive Models” by T.J. Hastie and R.J. Tibshirani [2].

MOJO Support

GAM supports importing and exporting MOJOs.

Defining a GAM Model

Parameters are optional unless specified as required. GAM shares many GLM parameters.

Algorithm-specific parameters

• bs: An array specifying the spline types for each GAM predictor. You must include one value for each GAM predictor. One of:

  • 0 (default) specifies cubic regression spline.

  • 1 specifies thin plate regression with knots.

  • 2 specifies monotone splines (or I-splines).

  • 3 specifies NBSplineTypeI M-splines (which can support any polynomial order).

• gam_columns: Required An array of column names representing the smoothing terms used for prediction. GAM will build a smoother for each specified column.

• keep_gam_cols: Specify whether to save keys storing GAM columns. This option defaults to False (disabled).

• knot_ids: A string array storing frame keys/IDs that contain knot locations. Specify one value for each GAM column specified in gam_columns.

• num_knots: An array that specifies the number of knots for each predictor specified in gam_columns.

• scale: An array specifying the smoothing parameter for GAM. If specified, must be the same length as gam_columns.

• scale_tp_penalty_mat: Scale penalty matrix for thin plate smoothers. This option defaults to False.

• splines_non_negative: (Applicable for I-spline or bs=2 only) Set this option to True if the I-splines are monotonically increasing (or monotonically non-decreasing). Set this option to False if the I-splines are monotonically decreasing (or monotonically non-increasing). If specified, this option must be the same size as gam_columns. Values for other spline types will be ignored. This option defaults to True (enabled).

• spline_orders: Order of I-splines (also known as monotone splines) and NBSplineTypeI M-splines used for GAM predictors. For I-splines, the spline_orders will be the same as the polynomials used to generate the splines. For M-splines, the polynomials will be spline_orders \(-1\). For example, spline_orders=3 for I-splines means a polynomial of order 3 will be used in the splines while for M-splines it means a polynomial of order 2 will be used. If specified, this option must be the same size as gam_columns. Values for bs=0 or bs=1 will be ignored.

• standardize_tp_gam_cols: Standardize thin plate predictor columns. This option defaults to False.

Common parameters

• auc_type: Set the default multinomial AUC type. Must be one of:

  • "AUTO" (default)

  • "NONE"

  • "MACRO_OVR"

  • "WEIGHTED_OVR"

  • "MACRO_OVO"

  • "WEIGHTED_OVO"

• early_stopping: Specify whether to stop early when there is no more relative improvement on the training or validation set. This option defaults to True (enabled).

• export_checkpoints_dir: Specify a directory to which generated models will automatically be exported.

• fold_assignment: (Applicable only if a value for nfolds is specified and fold_column is not specified) Specify the cross-validation fold assignment scheme. One of:

  • AUTO (default; uses Random)

  • Random

  • Modulo (read more about Modulo)

  • Stratified (which will stratify the folds based on the response variable for classification problems)

• fold_column: Specify the column that contains the cross-validation fold index assignment per observation.

• ignore_const_cols: Enable this option to ignore constant training columns since no information can be gained from them. This option defaults to True (enabled).

• ignored_columns: (Python and Flow only) Specify the column or columns to be excluded from the model. In Flow, click the checkbox next to a column name to add it to the list of columns excluded from the model. To add all columns, click the All button. To remove a column from the list of ignored columns, click the X next to the column name. To remove all columns from the list of ignored columns, click the None button. To search for a specific column, type the column name in the Search field above the column list. To only show columns with a specific percentage of missing values, specify the percentage in the Only show columns with more than 0% missing values field. To change the selections for the hidden columns, use the Select Visible or Deselect Visible buttons.

• keep_cross_validation_fold_assignment: Enable this option to preserve the cross-validation fold assignment. This option defaults to False (disabled).

• keep_cross_validation_models: Specify whether to keep the cross-validated models. Keeping cross-validation models may consume significantly more memory in the H2O cluster. This option defaults to True (enabled).

• keep_cross_validation_predictions: Specify whether to keep the cross-validation predictions. This option defaults to False (disabled).

• max_active_predictors: Specify the maximum number of active predictors during computation. This value is used as a stopping criterium to prevent expensive model building with many predictors. This value defaults to -1 (unlimited). This default indicates that if the IRLSM solver is used, the value of max_active_predictors is set to 5000, otherwise it is set to 100000000.

• max_iterations: Specify the number of training iterations. This option defaults to -1 (unlimited).

• max_runtime_secs: Maximum allowed runtime in seconds for model training. Use 0 (default) to disable.

• missing_values_handling: Specify how to handle missing values (one of: Skip, MeanImputation (default), or PlugValues).

• model_id: Specify a custom name for the model to use as a reference. By default, H2O automatically generates a destination key.

• nfolds: Specify the number of folds for cross-validation. The value can be 0 (default) to disable or \(\geq\) 2.

• offset_column: Specify a column to use as the offset; the value cannot be the same as the value for the weights_column.

  Note: Offsets are per-row “bias values” that are used during model training. For Gaussian distributions, they can be seen as simple corrections to the response (y) column. Instead of learning to predict the response (y-row), the model learns to predict the (row) offset of the response column. For other distributions, the offset corrections are applied in the linearized space before applying the inverse link function to get the actual response values.

• score_each_iteration: Enable this option to score during each iteration of the model training. This option defaults to False (disabled).

• seed: Specify the random number generator (RNG) seed for algorithm components dependent on randomization. The seed is consistent for each H2O instance so that you can create models with the same starting conditions in alternative configurations. This option defaults to -1 (time-based random number).

• standardize: Specify whether to standardize the numeric columns to have a mean of zero and unit variance. Standardization is highly recommended; if you do not use standardization, the results can include components that are dominated by variables that appear to have larger variances relative to other attributes as a matter of scale, rather than true contribution. This option defaults to False (disabled).

• stopping_metric: Specify the metric to use for early stopping. The available options are:

  • AUTO (default): (This defaults to logloss for classification and deviance for regression)

  • deviance

  • logloss

  • MSE

  • RMSE

  • MAE

  • RMSLE

  • AUC (area under the ROC curve)

  • AUCPR (area under the Precision-Recall curve)

  • lift_top_group

  • misclassification

  • mean_per_class_error

• stopping_rounds: Stops training when the option selected for stopping_metric doesn’t improve for the specified number of training rounds, based on a simple moving average. To disable this feature, specify 0 (default).

  Note: If cross-validation is enabled:

  • All cross-validation models stop training when the validation metric doesn’t improve.

  • The main model runs for the mean number of epochs.

  • N+1 models may be off by the number specified for stopping_rounds from the best model, but the cross-validation metric estimates the performance of the main model for the resulting number of epochs (which may be fewer than the specified number of epochs).

• stopping_tolerance: Specify the relative tolerance for the metric-based stopping to stop training if the improvement is less than this value. This option defaults to 0.001.

• training_frame: Required Specify the dataset used to build the model.

  NOTE: In Flow, if you click the Build a model button from the Parse cell, the training frame is entered automatically.

• validation_frame: Specify the dataset used to evaluate the accuracy of the model.

• weights_column: Specify a column to use for the observation weights, which are used for bias correction. The specified weights_column must be included in the specified training_frame.

  Python only: To use a weights column when passing an H2OFrame to x instead of a list of column names, the specified training_frame must contain the specified weights_column.

  Note: Weights are per-row observation weights and do not increase the size of the data frame. This is typically the number of times a row is repeated, but non-integer values are supported as well. During training, rows with higher weights matter more due to the larger loss function pre-factor.

• x: Specify a vector containing the names or indices of the predictor variables to use when building the model. If x is missing, then no predictors will be used.

• y: Required Specify the column to use as the dependent variable.

  • For a regression model, this column must be numeric (Real or Int).

  • For a classification model, this column must be categorical (Enum or String). If the family is Binomial, the dataset must contain two levels.

A Simple Linear Model

Consider \(n\) observations, \(x_i\) with response variable \(y_i\), where \(y_i\) is an observation on random variable \(Y_i\). Let \(u_i ≡ E(Y_i)\). Assuming a linear relationship between the predictor variables and the response, the following relationship exists between \(xi\) and \(Y_i\) as:

\(Y_i = u_i + \epsilon_i \text{ where } u_i = \beta_i x_i + \beta_0\)

and \(\beta_i, \beta_0\) are unknown parameters, \(\epsilon_i\) are i.i.d zero mean variables with variances \(\delta^2\). We already know how to estimate \(\beta_i, \beta_0\) using GLM.

A Simple Linear GAM Model

Using the same observations as in the previous A Simple Linear Model section, a linear GAM model can be:

\(Y_i = f(x_i) + \epsilon_i \text{ where } f(x_i) = {\Sigma_{j=1}^k}b_j(x_i)\beta_j+\beta_0\)

Again, \(\beta = [\beta_0, \beta_1, \ldots, b_k]\) is an unknown parameter vector that can also be estimated using GLM. This can be done by using \([b_1(x_i), b_2(x_i), \ldots , b_K(x_i)]\) as the predictor variables instead of \(x_i\). Here, we are basically estimating \(f(x_i)\) using a set of basis functions:

\(\{b_1(x_i), b_2(x_i), \ldots, b_K(x_i)\}\)

where \(k\) is the number of basis functions used. Note that for each predictor variable, we get to decide the types and number of basis functions that we would like to use to best generate a GAM.

A Simple Piecewise Linear Basis Function

To understand the role of basis functions, we are going to use a linear tent function.

Using piecewise basis functions, we need to pay attention to the locations of the function’s derivative discontinuities, that is by the locations at which the linear pieces join up. These locations are referred to as the knots and denoted by \(\{x_i^*:j=1, \ldots, K\}\). And suppose that the knots are sorted, meaning that \(x_i^* > x_{i-1}^*\). Then for \(j=2, \ldots, K - 1\), we have basis function \(b_j(x)\) defined as:

Using Piecewise Tent Function to Approximate One Predictor Variable

To illustrate how we can use the piecewise tent functions to approximate a predictor variable, let’s use the following example for a predictor:

• Predictor value goes from 0.0 to 1.0

• Set \(K=10\) to use 10 piecewise tent functions

• The knots are located at 0, 1/9, 2/9, 3/9, …, 8/9, 1.

The basis function values are plotted in in the figure below. Note that there are 10 basis functions. The basis function values overlap with its neighbors from the left and the right except for the first and the last basis functions.

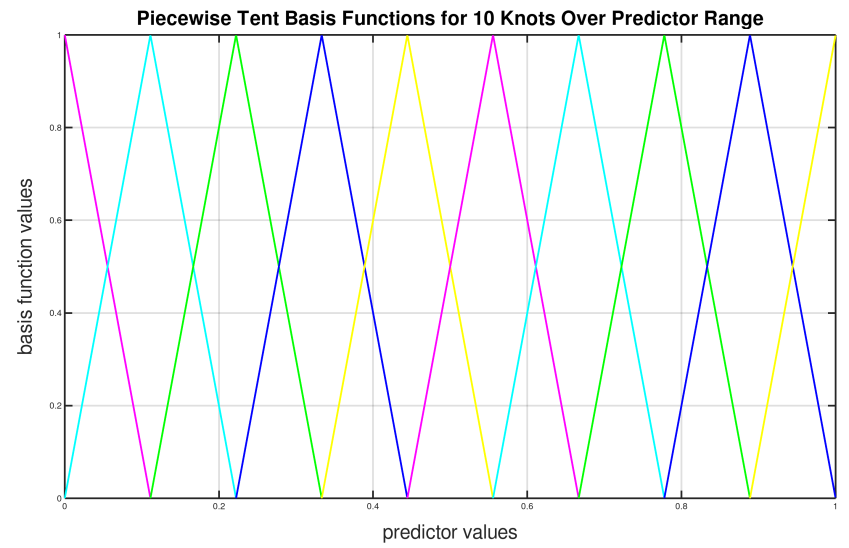
For simplicity, let’s assume that we only have 21 predictor values uniformly spreading over the range from 0 to 1 with values 0, 0.05, 0.1, 0.15, …, 1.0. The next task is to translate each \(x_j\) to a set of 10 basis function values. This means that for every value of \(x_j\), we will obtain 10 values, each one correspond to each of the basis function.

For the predictor value at 0, the only basis function that matters is the first one. All the other basis function contributes 0 to the predictor value. Hence, for \(x_j = 0\), the vector corresponding to all basis functions will have the following values: {1,0,0,0,0,0,0,0,0,0} because the first basis function value is 1 at \(x_j = 0\). Note Substitute \(x=0\) to the first basis function

\(b_1(x) = \frac{\big(\frac{1}{9} - x \big)}{\big(\frac{2}{9} - \frac{1}{9} \big)}\)

For predictor value 0.05, only the first and second basis functions contribute to its value, while the other basis functions are 0 at 0.05. The value of the first basis function is 0.55. Note Substitute \(x=0.05\) to the first basis function

\(b_1(x) = \frac{\big(\frac{1}{9} - x \big)}{\big(\frac{2}{9} - \frac{1}{9} \big)}\)

The value of the second basis function at 0.05 is 0.45. Note Substitute \(x=0.05\) to the second basis function

\(b_2(x) = \frac{x}{\big(\frac{1}{9}\big)}\)

Hence, for \(x_j = 0.05\), the vector corresponding to all basis function is {0.55,0.45,0,0,0,0,0,0,0,0}.

We have calculated the expanded basis function vector for all predictor values, and they can be found in following table.

\(x_j\)	\(b_1\)	\(b_2\)	\(b_3\)	\(b_4\)	\(b_5\)	\(b_6\)	\(b_7\)	\(b_8\)	\(b_9\)	\(b_{10}\)
0	1	0	0	0	0	0	0	0	0	0
0.05	0.55	0.45	0	0	0	0	0	0	0	0
0.1	0.1	0.9	0	0	0	0	0	0	0	0
0.15	0	0.65	0.35	0	0	0	0	0	0	0
0.2	0	0.2	0.8	0	0	0	0	0	0	0
0.25	0	0	0.75	0.25	0	0	0	0	0	0
0.3	0	0	0.3	0.7	0	0	0	0	0	0
0.35	0	0	0	0.85	0.15	0	0	0	0	0
0.4	0	0	0	0.4	0.6	0	0	0	0	0
0.45	0	0	0	0	0.95	0.05	0	0	0	0
0.5	0	0	0	0	0.5	0.5	0	0	0	0
0.55	0	0	0	0	0.05	0.95	0	0	0	0
0.6	0	0	0	0	0	0.6	0.4	0	0	0
0.65	0	0	0	0	0	0.15	0.85	0	0	0
0.7	0	0	0	0	0	0	0.7	0.3	0	0
0.75	0	0	0	0	0	0	0.25	0.75	0	0
0.8	0	0	0	0	0	0	0	0.8	0.2	0
0.85	0	0	0	0	0	0	0	0.35	0.65	0
0.9	0	0	0	0	0	0	0	0	0.9	0.1
0.95	0	0	0	0	0	0	0	0	0.45	0.55
1	0	0	0	0	0	0	0	0	0	1

Spline Functions

It has been proven in [2] that the natural cubic splines are the smoothest interpolators. For a set of points \({x_i, y_i:i = 1, \ldots, n}\) where \(x_i \leq x_{i+1}\). The natural cubic spline, \(g(x)\), interpolating these points, is a function made up of sections of cubic polynomial, one for each \([x_i, x_{i+1}]\). They are joined up together so that the whole spline is continuous to second derivative, while \(g(x_i) = y_i\) and \(g^{''}(x_i) = g^{''}(x_n) = 0\). To ensure smooth function, we can add a penalty function \(J(f) = \int_{x_1}^{x_n} {(f^{''}(x))^2}dx\) to the actual objective function that we are trying to optimize. The rationality behind this penalty is that the second derivative of a function measures the gradient change. For functions that wriggle a lot, it will have a higher second derivative magnitude. For a straight line that does not wriggle at all, the second derivative is zero.

Cubic Regression Splines

Following the implementation in [1], we have implemented the cubic regression splines for a single predictor variable. This approach defines the splines in terms of its values at the knots. Next, we define a cubic spline function, \(f(x)\), \(k\) knots, \(x_1, x_2, \ldots, x_k\). Let \(\beta_j = f(x_j)\) and \(\delta_j = f^{''}(x_j) = \frac{d^2f(x_j)}{d^2x}\).

The splines can be written as:

\[f(x) = a_j^-(x)\beta_j + a_j^+(x)\beta_{j+1} + c_j^-(x)\delta_j + c_j^+(x) \delta_{j+1} \text{ for } x_j \leq x \leq x_{j+1}\]

where:

• \(a_j^-(x) = (x_{j+1} - x)/h_j, a_j^+(x) = (x - x_j) / h_j\)

• \(c_j^-(x) = \big[\frac{(x_{j+1}-x)^3}{h_j} - h_j(x_{j+1} - x)\big] /6, c_j^+(x) = \big[\frac{(x-x_j)^3}{h_j} - h_j(x-x_j \big] / 6\)

Note that in order to ensure smooth fitting functions at the knots, the spline must be continuous to second derivative at the \(x_j\) and should have zero second derivative at \(x_1\) and \(x_k\). It can be shown that \(\beta\delta^- = DB\) (to be added at a later date), where

Let \(BinvD = B^{-1}D\) and let \(F = {\begin{bmatrix}0\\BinvD\\0\end{bmatrix}}\)

The spline can be rewritten entire in terms of \(\beta\) as

\(f(x) = a_j^-(x)\beta_j + a_j^+(x)\beta_{j+1} + c_j^-(x)F_j\beta + c_j^+(x)F_{j+1}\beta \text{ for } x_j \leq x \leq x_{j+1}\)

which can be written as \(f(x_i) = \sum_{j=1}^{k}b_j(x_i)\beta_j+\beta_0\) where \(b_j(x_i)\) are the basis functions and \(\beta_0, \beta_1, \ldots, \beta_k\) are the unknown parameters that can be estimated using GLM. In addition, the penalty term added to the final objective function can be derived to be:

\[\int_{x_1}^{x_k} (f^{''}(x))^2dx = \beta^T D^T B^{-1} D\beta = \beta^T D^T BinvD\beta = \beta^T S\beta\]

where \(S = D^T B^{-1} D\)

For linear regression models, the final objective function to minimize is

\[\sum_{i=1}^n \bigg( y_i - \big( \sum_{j=1}^k b_j(x_i)\beta_j + \beta_0 \big) \bigg) + \lambda \beta^T S \beta\]

Note that \(\lambda\) will be another parameter for the user to choose using gridsearch. In a future release, we may use cross-validation to automatically choose \(lambda\).

Hence, at this point, we can call our GLM. However, we still need to add the contribution of the penalty term to the gradient and hessian calculation.

Thin Plate Regression Splines

For documentation on thin plate regression splines, refer here:

• GAM Thin Plate Regression Spline

Monotone Splines

We have implemented I-splines which are used as monotone splines. Monotone splines do not support multinomial or ordinal families. In order to specify the monotone spline, you need to both set bs = 2 and specify spline_orders which will be equal to the polynomials used to generate the splines.

B-splines: \(Q_{i,k}(t)\)

This implementation begins with the B-spline. Let \(Q_{i,k}(t)\) denote a B-spline of order \(k\) at knot \(i\) where it is non-zero over the duration \(t_i \leq t < t_{i+k}\). The recursive formula [4] used to generate a B-spline of a higher order from two B-splines of a lower order is:

\[Q_{i,k}(t) = {\frac{(t-t_{i})}{(t_{i+k}-t_{i})}} Q_{i,k-1}(t) + {\frac{(t_{i+k}-t)}{(t_{i+k}-t_{i})}} Q_{i+1,k-1}(t)\]

Using knotes \(t_0,t_1,\dots ,t_N\) over the range of inputs of interest from \(t_0\) to \(t_N\), an order 1 B-spline is defined as [4]:

\[\begin{split}Q_{i,1}(t) = \begin{cases}{\frac{1}{(t_{i+1}-t_i)}},t_i \leq t < t_{i+1} \\ 0,t<t_i \text{ or } t \geq t_{i+1} \\\end{cases}\end{split}\]

Extending the number of knots

To generate higher order splines, you have to extend the original knots \(t_0,t_1,\dots ,t_N\) over the range of inputs of interest. You do this by adding \(k-1\) knots of value \(t_0\) to the front of the knots and \(k-1\) knots of value \(t_N\) to the end of the knots. The new duplication will look like:

\[t_0,t_0,\dots ,t_0,t_1,t_2,\dots ,t_{N-1},t_N,t_N,\dots ,t_N\]

where:

• \(t_0,t_0,\dots ,t_0\) and \(t_N,t_N,\dots ,t_N\) are the \(k\) duplicates.

The formula we used to calculate the number of basis functions over the original knots \(t_0,t_1,\dots ,t_N\) is:

\[N+1+k-2\]

where:

• \(N+1\) is the number of knots over the input range without duplication

• \(k\) is the order of the spline

M-splines: \(M_{i,k}(t)\)

M-splines serve two functions: they are part of the construction of I-splines and they are normal (non-monotonic) splines that are implemented separate of the monotone spline as part of the GAM toolbox. You must set bs = 3 for M-splines. spline_orders must also be set where the polynomials used to generate the splines will be equal to spline_orders-1. If you set spline_orders = 1 then you must set num_knots >= 3.

The B-spline function can be normalized and denoted as \(M_{i,k}(t)\) where it has an integration of 1 over the range of interest and is non-zero. This is the normalized B-spline Type I, and it is defined as:

\[M_{i,k}(t) = k \times Q_{i,k}(t)\]

with the property \(\int_{- \infty}^{+ \infty} M_{i,k}(t)dt = \int_{t_i}^{t_{i+k}} M_{i,k}(t)dt = 1\).

You can derive \(M_{i,k}(t)\) using the following recursive formula:

\[M_{i,k}(t) = \frac{k}{k-1} \bigg(\frac{(t-t_1)}{(t_{i+k}-t_i)} M_{i,k-1}(t) + \frac{(t_{i+k}-t)}{(t_{i+k}-t_i)} M_{i+1,k-1}(t) \bigg)\]

Note that \(M_{i,k}(t)\) is defined over the same knot sequence as the original B-spline, and the number of \(M_{i,k}(t)\) splines is the same as the number of B-splines over the same known sequence.

N-splines: \(N_{i,k}(t)\)

The N-splines are normalized to have a summation of 1 when \(t_0 \leq t < t_N\) as \(\sum_{i=0}^{N+k-1}N_{i,k}(t) = 1\). \(N_{i,k}(t)\) is the normalized B-spline Type II in this implementation. The N-splines share the same knot sequence with the original M-spline and B-spline. The N-spline can be derived from the M-spline or the B-spline using:

\[N_{i,k}(t) = {\frac{(t_{i+k}-t_i)}{k}}M_{i,k}(t) = (t_{i+k}-t_i)Q_{i,k}(t)\]

Or, you can use the recursive formula where higher order N-splines can be derived from two lower order N-splines:

\[N_{i,k}(t) = {\frac{t-t_i}{t_{i+k-1}-t_i}}N_{i,k-1}(t)+{\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}}N_{i+1,k-1}(t)\]

I-splines: \(I_{i,k}(t)\)

I-splines are used to build the monotone spline functions by restricting the gamified column coefficients to be \(\geq\) 0 [5]. We have implemented I-splines using the following method:

\[I_{i,k}(t) = \sum_{l=1}^{i+r}N_{l,k+1}(t), t \leq t_{i+r+1}\]

Penalty Matrix

The objective function used to derive the coefficients for regression is:

\[\sum_{i=0}^n \Bigg(y_i- \bigg(\sum_{j=0}^{numBasis-1}I_{j,k}(t_i)\beta_j + \beta_0 \bigg)\Bigg)^2 + \lambda\beta^T penaltyMat\beta\]

The second derivative of all basis functions is defined as:

\[\begin{split}I_k^{2ndDeriv} = \begin{bmatrix} {\frac{d^2(I_{0,k}(t))}{d^2t}} \\ {\frac{d^2(I_{1,k}(t))}{d^2t}} \\ \vdots \\ {\frac{d^2(I_{numBasis-2,k}(t))}{d^2t}} \\ {\frac{d^2(I_{numBasis-1,k}(t))}{d^2t}} \\\end{bmatrix}\end{split}\]

where the penalty matrix (\(penaltyMat\)) for I-spline \(I_{j,k}(t)\) is defined as:

\[penaltyMat = \int_{t_0}^{t_N}I_k^{2ndDeriv} \times \text{ transpose of }(I_k^{2ndDeriv})dt\]

Element at row \(m\) and column \(n\) of \(penaltyMat\) is

\[penaltyMat_{m,n} = \int_{t_0}^{t_N}{\frac{d^2(I_{m,k}(t))}{d^2t}}{\frac{d^2(I_{n,k}(t))}{d^2t}}dt\]

Derivative of M-splines

The penalty matrix written in terms of the second derivative of M-spline as:

\[penaltyMat_{m,n} = \int_{t_0}^{t_N} \frac{d^2M_{m,k} (t)}{dt^2} \frac{d^2M_{n,k} (t)}{dt^2}dt\]

Instead of using the recursive expression, look at the coefficients associated with \(M_{m,k}(t)\), take the second derivative, and go from there. This is the procedure to use:

• generate the coefficients of \(\frac{d^2M_{i,k}(t)}{dt^2}\);

• implement multiplication of coefficients of \(\frac{d^2M_{i,k} (t)}{dt^2} \frac{d^2M_{j,k} (t)}{dt^2}dt\). Due to the commutative property, \(\frac{d^2M_{i,k} (t)}{dt^2} \frac{d^2M_{j,k} (t)}{dt^2}dt = \frac{d^2M_{j,k} (t)}{dt^2}dt \frac{d^2M_{i,k} (t)}{dt^2}\), so you only need to perform the multiplication once and the \(penaltyMat_{m,n}\) is symmetrical;

• implement the integration of \(\frac{d^2M_{i,k}(t)}{dt^2} \frac{d^2M_{j,k}(t)}{dt^2}\) by easy integration of the coefficients.

General GAM

In a general GAM, using the GLM jargon, the link function can be constructed using a mixture of predictor variables and smooth functions of predictor variables as follows:

\[g(u_i) = \beta_0 + \beta_1 x_{1i} + \cdots + \beta_mx_{mi} + \sum_{j=1}^{k_1}b_j^i(x_{li})\beta_{m+j} + \cdots + \sum_{j=1}^{k_q}b_j^q(x_{li})\beta_{m+k_1+\cdots+k_{q-1} + j}\]

This is the GAM we implemented in H2O. However, with multiple predictor variables in any form, we need to resolve the identifiability problems by adding identifiability constraints.

Identifiability Constraints

Consider GAM with multiple predictor smooth functions like the following:

\[y_i = a+f_1(x_i) + f_2(v_1) + \epsilon_i\]

The model now contains more than one function introduces an identifiability problem: \(f_1\) an \(f_2\) are each only estimable to within an additive constant. This is due to the fact that \(f_1(x_i) + f_2(v_i) = (f_1(x_i) + C) + (f_2(v_i) - C)\). Hence, identifiability constraints have to be imposed on the model before fitting to avoid the identifiability problem. The following sum-to-zero constraints are implemented in H2O:

\[\sum_{i=1}^n f_p(x_i) = 0 = 1^Tf_p\]

where 1 is a column vector of 1, and \(f_p\) is the column vector containing \(f_p(x_1), \ldots ,f_p(x_n)\). To apply the sum-to-zero constraints, a Householder transform is used. Refer to [1] for details. This transform is applied to each basis function of any predictor column we choose on its own.

Note: this does not apply to monotone splines because the coefficients for these splines must be \(\geq 0\).

Sum-to-zero Constraints Implementation

Let \(X\) be the model matrix that contain the basis functions of one predictor variable, the sum-to-zero constraints required that

\[1^Tf_p = 0 = 1^TX\beta\]

where \(\beta\) contains the coefficients relating to the basis functions of that particular predictor column. The idea is to create a \(k \text{ by } (k-1)\) matrix \(Z\) such that \(\beta = Z\beta_z\), then \(1^TX\beta =0\) for any \(\beta_z\). To see how this works, let’s go through the following derivations:

• With \(Z\), we are looking at \(0 = 1^TX\beta = 1^TXZ\beta_z\)

• Let \(C=1^TX\), then the QR decomposition of \(C^T = U {\begin{bmatrix}P\\0\end{bmatrix}}\) where \(C^T\) is of size \(k \times 1\), \(U\) is of size \(k \times k\), \(P\) is the size of \(1\times1\)

• Substitute everything back to \(1^TXZ\beta_z = [P^T \text{ } 0]{\begin{bmatrix}D^T\\Z^T\end{bmatrix}} Z\beta_z = [P^T \text{ } 0]{\begin{bmatrix}D^TZ\beta_z\\Z^TZ\beta_z\end{bmatrix}} = P^TD^TZ\beta_z + 0Z^TZ\beta_z=0\) since \(D^TZ=0\)

Generating the Z Matrix

One Householder reflection is used to generate the \(Z\) matrix. To create the \(Z\) matrix, we need to calculate the QR decomposition of \(C^T = X^T1\) Since \(C^T\) is of size \(k \times 1\), the application of one householder reflection will generate \(HC^T = {\begin{bmatrix}R\\0\end{bmatrix}}\) where \(R\) is of size \(1 \times 1\). This implies that \(H = Q^T = Q\), since the householder reflection matrix is symmetrical. Hence, computing \(XZ\) is equivalent to computing \(XH\) and dropping the first column.

Generating the Householder reflection matrix H

Let \(\bar{x} = X^T1\) and \(\bar{x}' = {\begin{bmatrix}{\parallel{\bar{x}}\parallel}\\0\end{bmatrix}}\), then \(H = (I - \frac{2uu^T}{(u^Tu)})\) and \(u = \bar{x} = \bar{x}'\).

Estimation of GAM Coefficients with Identifiability Constraints

The following procedure is used to estimate the GAM coefficients:

• Generating \(Z\) matrix for each predictor column that uses smoothe functions

• Generate new model matrix for each predictor column smooth function as \(X_z = XZ\), new penalty function \({\beta{^T_z}}Z^TSZ\beta_z\).

• Call GLM using model matrix \(X_z\), penalty function \({\beta{^T_z}}Z^TSZ\beta_z\) to get coefficient estimates of \(\beta_z\)

• Convert \(\beta_z\) to \(\beta\) using \(\beta = Z\beta_z\) and performing scoring with \(\beta\) and the original model matrix \(X\).

Examples

Below are simple examples showing how to use GAM in R and Python.

General GAM

R

Python

library(h2o)
h2o.init()

# create frame knots
knots1 <- c(-1.99905699, -0.98143075, 0.02599159, 1.00770987, 1.99942290)
frame_Knots1 <- as.h2o(knots1)
knots2 <- c(-1.999821861, -1.005257990, -0.006716042, 1.002197392, 1.999073589)
frame_Knots2 <- as.h2o(knots2)
knots3 <- c(-1.999675688, -0.979893796, 0.007573327, 1.011437347, 1.999611676)
frame_Knots3 <- as.h2o(knots3)

# import the dataset
h2o_data <- h2o.importFile("https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/multinomial_10_classes_10_cols_10000_Rows_train.csv")

# Convert the C1, C2, and C11 columns to factors
h2o_data["C1"] <- as.factor(h2o_data["C1"])
h2o_data["C2"] <- as.factor(h2o_data["C2"])
h2o_data["C11"] <- as.factor(h2o_data["C11"])

# split into train and test sets
splits <- h2o.splitFrame(data = h2o_data, ratios = 0.8)
train <- splits[[1]]
test <- splits[[2]]

# Set the predictor and response columns
predictors <- colnames(train[1:2])
response <- 'C11'

# specify the knots array
numKnots <- c(5, 5, 5)

# build the GAM model
gam_model <- h2o.gam(x = predictors,
                     y = response,
                     training_frame = train,
                     family = 'multinomial',
                     gam_columns = c("C6", "C7", "C8"),
                     scale = c(1, 1, 1),
                     num_knots = numKnots,
                     knot_ids = c(h2o.keyof(frame_Knots1), h2o.keyof(frame_Knots2), h2o.keyof(frame_Knots3)))

# get the model coefficients
coefficients <- h2o.coef(gam_model)

# generate predictions using the test data
pred <- h2o.predict(object = gam_model, newdata = test)

import h2o
from h2o.estimators.gam import H2OGeneralizedAdditiveEstimator
h2o.init()

# create frame knots
knots1 = [-1.99905699, -0.98143075, 0.02599159, 1.00770987, 1.99942290]
frameKnots1 = h2o.H2OFrame(python_obj=knots1)
knots2 = [-1.999821861, -1.005257990, -0.006716042, 1.002197392, 1.999073589]
frameKnots2 = h2o.H2OFrame(python_obj=knots2)
knots3 = [-1.999675688, -0.979893796, 0.007573327,1.011437347, 1.999611676]
frameKnots3 = h2o.H2OFrame(python_obj=knots3)

# import the dataset
h2o_data = h2o.import_file("https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/multinomial_10_classes_10_cols_10000_Rows_train.csv")

# convert the C1, C2, and C11 columns to factors
h2o_data["C1"] = h2o_data["C1"].asfactor()
h2o_data["C2"] = h2o_data["C2"].asfactor()
h2o_data["C11"] = h2o_data["C11"].asfactor()

# split into train and validation sets
train, test = h2o_data.split_frame(ratios = [.8])

# set the predictor and response columns
y = "C11"
x = ["C1","C2"]

# specify the knots array
numKnots = [5,5,5]

# build the GAM model
h2o_model = H2OGeneralizedAdditiveEstimator(family='multinomial',
                                            gam_columns=["C6","C7","C8"],
                                            scale=[1,1,1],
                                            num_knots=numKnots,
                                            knot_ids=[frameKnots1.key, frameKnots2.key, frameKnots3.key])
h2o_model.train(x=x, y=y, training_frame=train)

# get the model coefficients
h2oCoeffs = h2o_model.coef()

# generate predictions using the test data
pred = h2o_model.predict(test)

GAM using Monotone Splines

R

Python

# Import the GLM test data:
gam_test = h2o.importFile("https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/binomial_20_cols_10KRows.csv")

# Split into train and validation sets:
splits <- h2o.splitFrame(data = gam_test, ratios = 0.8)
train <- splits[[1]]
test <- splits[[2]]

# Set the factors, predictors, and response:
gam_test["C1"] <- as.factor(gam_test["C1"])
gam_test["C2"] <- as.factor(gam_test["C2"])
gam_test["C21"] <- as.factor(gam_test["C21"])
predictors <- c("C1","C2")
response <- "C21"

# Build and train the model using spline order:
monotone_model <- h2o.gam(x = predictors, y = response,
                          training_frame = train,
                          family = 'binomial',
                          gam_columns = c("C11", "C12", "C13"),
                          scale = c(0.001, 0.001, 0.001),
                          bs = c(0, 2, 2),
                          num_knots = c(3, 4, 5),
                          spline_orders = c(2, 3, 4))

# Generate predictions using the test data:
pred <- h2o.predict(object = monotone_model, newdata = test)

# Import the GLM test data:
gam_test = h2o.import_file("https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/binomial_20_cols_10KRows.csv")

# Split into train and validation sets:
train, test = gam_test.split_frame(ratios = [.8])

# Set the factors, predictors, and response:
gam_test["C1"] = gam_test["C1"].asfactor()
gam_test["C2"] = gam_test["C2"].asfactor()
gam_test["C21"] = gam_test["C21"].asfactor()
predictors = ["C1","C2"]
response = "C21"

# Build and train your model using spline order:
monotone_model = H2OGeneralizedAdditiveEstimator(family="binomial",
                                                 gam_columns=["C11", "C12", "C13"],
                                                 scale=[0.001, 0.001, 0.001],
                                                 bs=[0,2,2],
                                                 spline_orders=[2,3,4],
                                                 num_knots=[3,4,5])
monotone_model.train(x=predictors, y=response, training_frame=train)

# Generate predictions using the test data:
pred = monotone_model.predict(test)

GAM using M-splines

R

Python

# Import the GLM test data set:
gam_test = h2o.importFile(“https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/binomial_20_cols_10KRows.csv”)

# Set the factors, predictors, and response:
gam_test["C1"] <- as.factor(gam_test["C1"])
gam_test["C2"] <- as.factor(gam_test["C2"])
gam_test["C21"] <- as.factor(gam_test["C21"])
predictors <- c("C1","C2")
response <- "C21"

# Split into train and validation sets:
splits <- h2o.splitFrame(data = gam_test, ratios = 0.8)
train <- splits[[1]]
test <- splits[[2]]

# Build and train the model using spline order:
mspline_model <- h2o.gam(x = predictors,
                         y = response,
                         training_frame = train,
                         family = "binomial"
                         gam_columns = c("C11", "C12", "C13"),
                         scale = c(0.001, 0.001, 0.001),
                         bs = c(2, 0, 3),
                         spline_orders = c(10, -1, 10),
                         num_knots = c(3, 4, 5))
# Retrieve the coefficients:
h2o.coef(mspline_model)

# Import the GLM test data set:
gam_test = h2o.import_file("https://s3.amazonaws.com/h2o-public-test-data/smalldata/glm_test/binomial_20_cols_10KRows.csv")

# Set the factors, predictors, and response:
gam_test["C1"] = gam_test["C1"].asfactor()
gam_test["C2"] = gam_test["C2"].asfactor()
gam_test["C21"] = gam_test["C21"].asfactor()
predictors = ["C1","C2"]
response = "C21"

# Split into train and validation sets:
train, test = gam_test.split_frame(ratios = [.8])

# Build and train your model using spline order:
mspline_model = H2OGeneralizedAdditiveEstimator(family="binomial",
                                                gam_columns=["C11", "C12", "C13"],
                                                scale=[0.001, 0.001, 0.001],
                                                bs=[2,0,3],
                                                spline_orders=[10,-1,10],
                                                num_knots=[3,4,5])
mspline_model.train(x=predictors, y=response, training_frame=train)

# Retrieve the coefficients:
coef = mspline_model.coef()
print(coef)

References

1. Simon N. Wood, Generalized Additive Models: An Introduction with R, Texts in Statistical Science, CRC Press, Second Edition.

2. T.J. Hastie, R.J. Tibshirani, Generalized Additive Models, Chapman and Hall, First Edition, 1990.

3. Lecture 7 Divided Difference Interpolation Polynomial by Professor R.Usha, Department of Mathematics, IITM, https://www.youtube.com/watch?v=4m5AKnseSyI .

4. Carl De Boor et. al., ON CALCULATING WITH B-SPLINES II. INTEGRATION, ResearchGate Article, January 1976.

5. J.O. Ramsay, “Monotone Regression Splines in Action”, Statistical Science, 1988, Vol. 3, No. 4, 425-461.