Random Forest¶

When to use RF¶

RF is a good choice when your objective is classification.

Defining a Model¶

Source:

The parsed data set to be used in training a model.

Response:

The dependent variable to be modeled.

Ignored Columns:

The set of features from the source data set to be omitted from training a model.

Classification:

An option that specifies the model to be a classifier when switched on.

Validation:

A .hex key associated with data to be used in validation of the model built using the data specified in Source.

N Trees:

The number of trees the user would like to generate for classification.

Max Depth:

A user defined tuning parameter for controlling model complexity (by number of edges); depth is the longest path from root to the furthest leaf. Maximum depth also specifies the maximum number of interactions that can be accounted for by the model.

Min Rows:

The minimum number of observations to be included in each terminal node. The maximum possible observations in a terminal node is N-1, where N is the number of observations. The minimum is 1, and is the case where each observation is in a unique terminal node.

N Bins:

A user defined tuning parameter for controlling model complexity. N bins sets the number of groups into which the original data can be split.

Score each iteration:

An option that returns an error rate for each iteration of the training process. It is used when models are especially complex. By producing a score for the model at each iteration, users can stop the training process when the cost of continuing to model is greater than the marginal gains in predictive power.

Importance:

An option that returns information about the importance of each feature in the overall model.

Mtries:

At each iteration a randomly chosen subset of the features in the training data are selected and evaluated to define the optimal split of that subset. Mtries specifies the number of features to be selected from the whole set. When set to -1 the number of features to be chosen is set to the square root of the total number of features, rounded to the nearest integer.

Seed:

A large number that allows the analyst to recreate an analysis by specifying a starting point for black box processes that would otherwise occur at a randomly chosen place within the data.

Build tree one node:

An option that allows users to train the model using one node, instead of using a distributed cluster with multiple nodes. Selecting this option can significantly impact the time it takes to train a model, and is recommended only for small data sets.

Interpreting Results¶

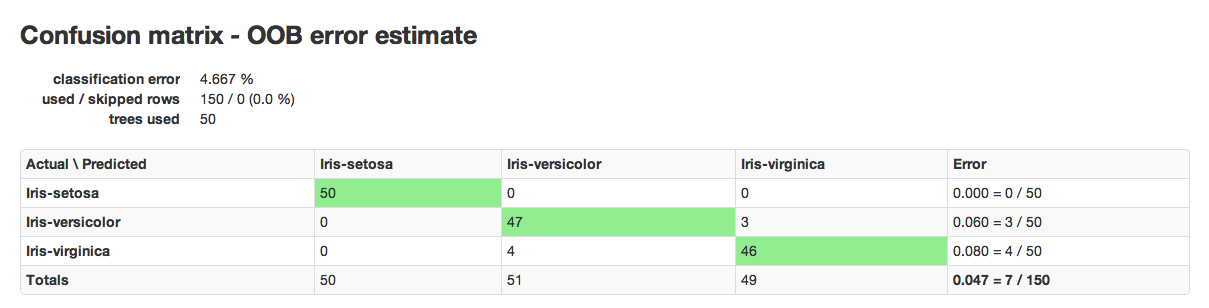
RF results are comprised of a model key and a confusion matrix. The model key specifies the full forest of trees to be used for predicting classifications.

An example of a confusion matrix is given below:

The highlighted fields across the diagonal indicate the number the number of true members of the class who were correctly predicted as true. In this case, of 111 total members of class F, 44 were correctly identified as class F, while a total of 80 observations were incorrectly classified as M or I, yielding an error rate of 0.654.

In the column for class F, 11 members of I were incorrectly classified as F, 56 as male, and a total of 111 observations in the set were identified as F.

The overall error rate is shown in the bottom right field. It reflects the total number of incorrect predictions divided by the total number of rows.

RF Error Rates¶

H₂O’s Random Forest Algo produces a dynamic confusion matrix. As each tree is built and OOBE (out of bag error estimate) is recalculated, expected behavior is that error rate increases before it decreases. This is a natural outcome of Random Forest’s learning process. When there are only a few trees, built on random subsets, the error rate is expected to be relatively high. As more trees are added, and thus more trees are “voting” for the correct classification of the OOB data, the error rate should decrease.