Principal Components Analysis¶
Principal Components Analysis (PCA) is closely related to Principal Components Regression. The algorithm is carried out on a set of possibly collinear features, and performs a transformation to produce a new set of uncorrelated features.
PCA is commonly used when users wish to model without regularization, or perform dimensionality reduction. It can also be useful to carry out before classification analysis like K-means, as K-means relies on Euclidian distances, and PCA guarantees that all dimensions of a manifold are orthogonal.
Defining a PCA Model¶
Source:
The .hex key associated with the parsed data to be used in the model.Ignored Columns:
The set of columns in the specified data set that should me omitted from the PCA. Selections are made by highlighting and selecting from the field, which populates when the data key is specified. In general PCA does not include categorical variables in analysis. Factors are treated as binomial columns, with an indicator for each factor level, less one reference level. If a variable is a factor, but has been coded as a number (for instance, color has been coded so that Green = 1, Red = 2, and Yellow = 3), users should be sure that these variables are not selected before running PCA. Including these variables can adversely impact results, because PCA will not correctly interpret them.Max PC:
An integer value indicating the maximum number of principal components to return.Tolerance:
A tuning parameter that allows the specification of a minimum level of variance accounted for. A tolerance set at X is a threshold for exclusion so that components with less than X times the standard deviation of the strongest predictive component are not included in results. For instance, for a tolerance of 2 if the standard deviation of the strongest predictor (the first component) is .39, than any subsequent component with standard deviation less than (2)(.39) = .78 will not be included in the analysis of principal components.Standardize:
Allows users to specify whether data should be transformed so that each column has a mean of 0 and a standard deviation of 1 prior to carrying out PCA. Standardizing is strongly recommended.
Interpreting Results¶
The results of PCA are presented as a table. An example of such a table is given below. In the simplest conceptual terms, PCA can be viewed as an algorithm that takes a given set of old variables, and performs transformations to yield a new set of variables. The new set of variables have useful practical application, as well as many desirable behaviors for further modeling.
Std Dev
Standard deviation. This is the standard deviation of the component defined in that column. In the example shown below the standard deviation of component PC0 is given as 2.5999.Prop Var
- Proportion of variance. This value signifies the proportion of
- variance in the overall data set accounted for by the component. In the example shown below the proportion of variance accounted for by PC0 is 76.5%.
Cum Prop Var
Cumulative proportion of variance. This value signifies the cumulative proportion accounted for by the set of principal components in descending order of contribution. For instance, in the example below the two strongest components are PC0 and PC1. PC0 accounts for about 76% of the variance in the dataset alone, while PC1 alone accounts for about 10% of variance. Together the two components account for 86% of variance; the value given in the Cum Prop Var field of the PC1 column.Variable Rows
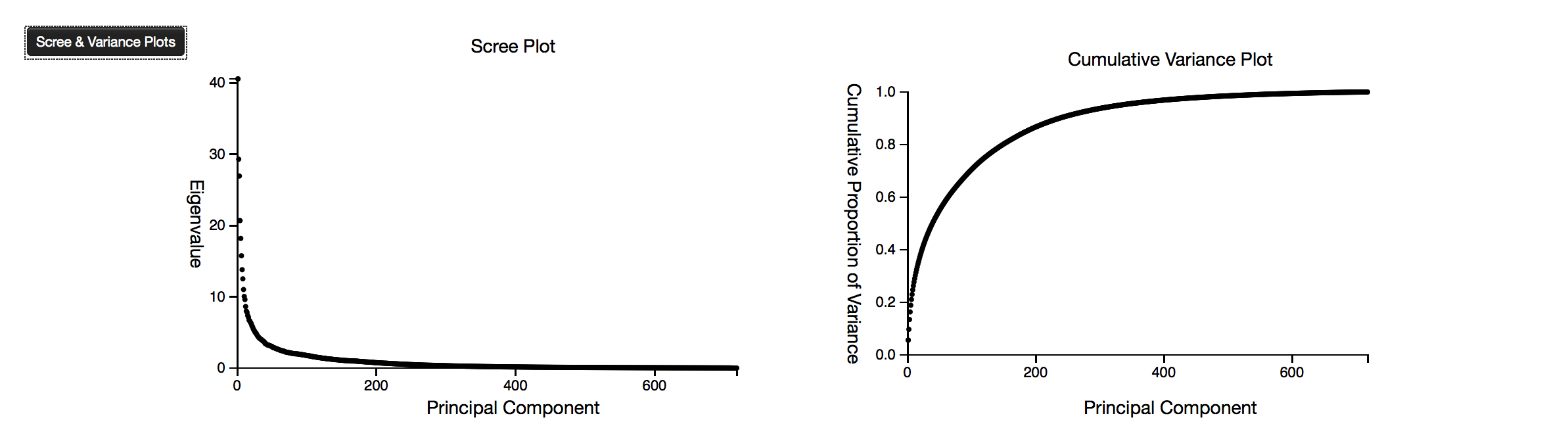
In the PCA results table the factors included in the composition of principal components are listed, and their contribution to the component is given (called factor loadings). Note that if the contributions are summed by the column, the absolute value of each of the factor loadings sum to the total variance of the principal component.Scree and Variance Plots
The scree and variance plots are visual tools that indicate the marginal contributions of each next principal component vector. The scree plot show the amount of variance accounted for by the first component, and then the additional variance accounted for by each of the next components, and approaches a minimum of zero contribution . The variance plot shows the cumulative variance accounted for by each of the components, and approaches a maximum value of 1.
Notes on the application of PCA¶
H2O’s PCA algorithm relies on a variance covariance matrix, not a correlation coefficient matrix. Covariance and correlation are related, but not equivalent. Specifically, the correlation between two variables is their normalized covariance. For this reason, it’s recommended that users standardize data before running a PCA analysis.
Additionally, modeling is driven by the simple assumption that set of derived variables can be appropriately characterized by a linear combination. PCA generates a set of new variables composed of combinations of the original variables. The variance explained by PCA is the covariance observed in the whole set of variables. If the objective of a PCA analysis is to use the new variables generated to predict an outcome of interest, that outcome must not be included in the PCA analysis. Otherwise, when the new variables are used to generate a model, the dependent variable will occur on both sides of the predictive equation.
PCA Algorithm “””””””””””””””””
Let \(X\) be an \(M\times N\) matrix where
- Each row corresponds to the set of all measurements on a particular attribute, and
- Each column corresponds to a set of measurements from a given observation or trial
The covariance matrix \(C_{x}\) is
\(C_{x}=\frac{1}{n}XX^{T}\)
where \(n\) is the number of observations.
\(C_{x}\) is a square, symmetric \(m\times m\) matrix, the diagonal entries of which are the variances of attributes, and the off diagonal entries are covariances between attributes.
The objective of PCA is to maximize variance while minimizing covariance.
To accomplish this suppose a new matrix \(C_{y}\) with off diagonal entries of 0, and each successive dimension of Y ranked according to variance.
PCA finds an orthonormal matrix \(P\) such that \(Y=PX\) constrained by the requirement that
\(C_{y}=\frac{1}{n}YY^{T}\)
be a diagonal matrix.
The rows of \(P\) are the principal components of X.
\(C_{y}=\frac{1}{n}YY^{T}\)
\(=\frac{1}{n}(PX)(PX)^{T}\)
\(C_{y}=PC_{x}P^{T}\).
Because any symmetric matrix is diagonalized by an orthogonal matrix of its eigenvectors, solve matrix \(P\) to be a matrix where each row is an eigenvector of \(\frac{1}{n}XX^{T}=C_{x}\)
Then the principal components of \(X\) are the eigenvectors of \(C_{x}\), and the \(i^{th}\) diagonal value of \(C_{y}\) is the variance of \(X\) along \(p_{i}\).
Eigenvectors of \(C_{x}\) are found by first finding the eigenvalues \(\lambda\) of \(C_{x}\).
For each eigenvalue \(lambda\) \((C-{x}-\lambda I)x =0\) where \(x\) is the eigenvector associated with \(\lambda\).
Solve for \(x\) by Gaussian elimination.